Graphs: topological sort

In many tasks it is important to do activities in a particular order. Otherwise they do not make sense. A good example is wearing clothes — putting on a hoodie before a t-shirt doesn’t make sense. Other examples are how people learn: we start from basic skills such as knowing letters, numbers, reading and writing, and then move on to more advanced subjects. Additionally, compilers must determine the order in which source files must be processed.

In simple terms, topological order is related to directed graphs and provides an order in which the graph must be traversed from “lower” to “greater” nodes, where greater means it is required to finish lower nodes before starting.

More mathematically, partial order is a relation R that satisfy for graph G:

\[\begin{aligned} &1.\space \forall u \in G \space u R u\\\ &2.\space \forall u \in G \space \space \forall v \in G \space \space u R v \land v R u \implies u = v\\\ &3.\space \forall u \in G \space \space \forall v \in G \space \space \forall w \in G \space \space u R v \land v R w \implies u R w \end{aligned}\]

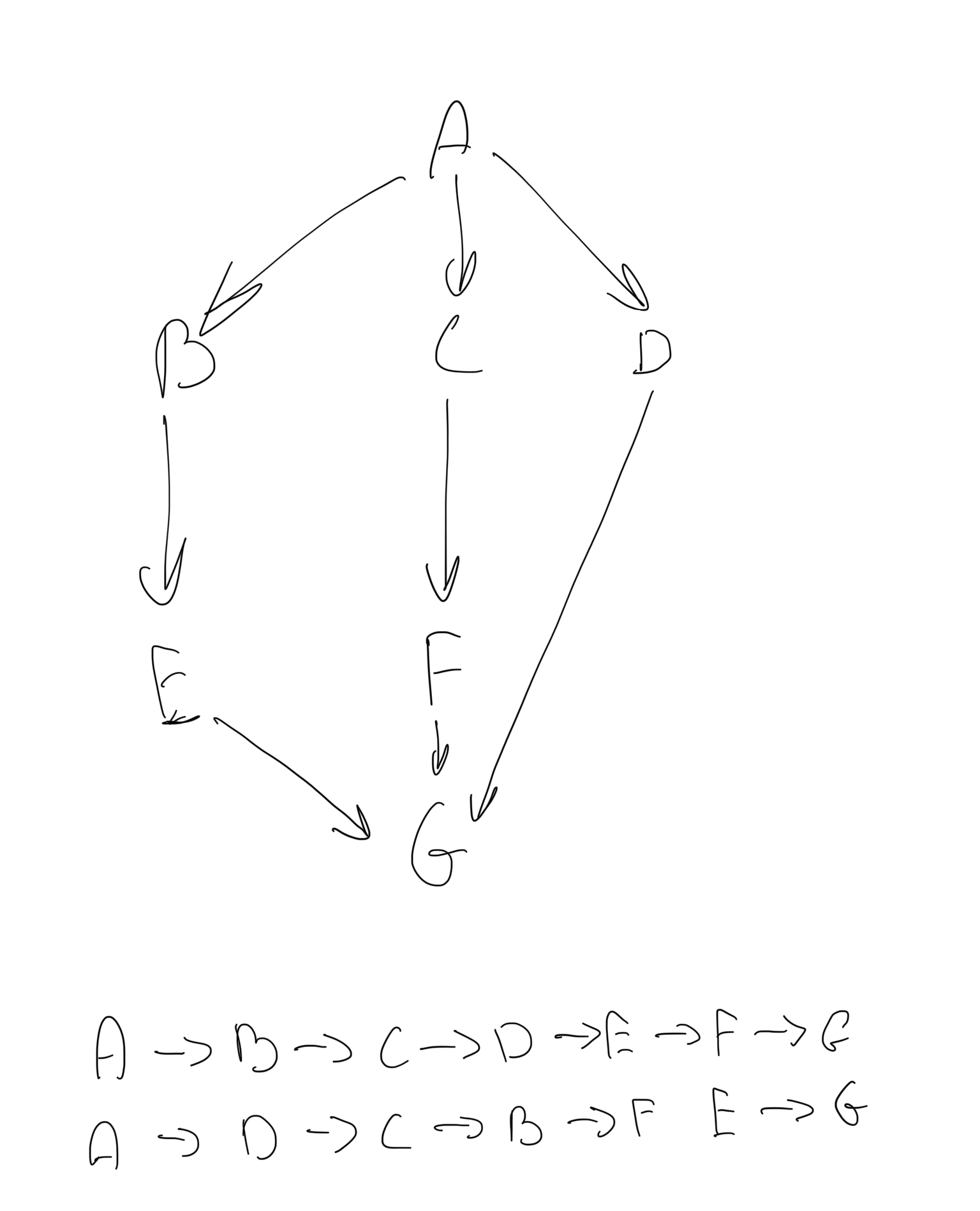
Example:

For the graph in the example, many valid orders exist — this is normal. Another important topological sort property is that it does not exist if the graph contains any cycle. The code that sorts graphs is almost identical to the code from the Graphs: directed graphs cycles post.

import scala.collection.mutable.{Set => MSet, Stack => MStack}


private def sortGraphRecursive(
      graph: Map[String, List[String]]
  ): List[String] = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]
    val result   = MStack.empty[String]

    def checkCycle(node: String): Boolean = {
      if (visited(node)) {
        false
      } else if (visiting(node)) {
        true
      } else {
        visiting.add(node)
        for (n <- graph(node)) {
          if (checkCycle(n)) {
            return true
          }
        }
        visiting.remove(node)
        visited.add(node)
        result.push(node)
        false
      }
    }

    for (n <- graph.keys) {
      if (checkCycle(n)) {
        return Nil
      }
    }

    result.toList
  }

import scala.collection.mutable.{Set => MSet, Stack => MStack}

 private def sortIterative(graph: Map[String, List[String]]): List[String] = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]
    val stack    = MStack.empty[String]
    val result   = MStack.empty[String]

    for (n <- graph.keys) {
      stack.push(n)
      while (stack.nonEmpty) {
        val cn = stack.pop()
        if (!visited(cn)) {
          val descendants = graph(cn)
          if (descendants.isEmpty || descendants.forall(visited)) {
            visiting.remove(cn)
            visited.add(cn)
            result.push(cn)
          } else if (visiting(cn)) {
            return Nil
          } else {
            visiting.add(cn)
            for (d <- descendants) {
              stack.push(d)
            }
          }
        }
      }
      visited.addAll(visiting)
      visiting.foreach(result.push)
      visiting.clear()
    }

    result.toList
  }

import scala.annotation.tailrec
import scala.collection.mutable.{Set => MSet, Stack => MStack}

private def sortTailRec(graph: Map[String, List[String]]): List[String] = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]
    val result   = MStack.empty[String]

    @tailrec
    def hasCycle(stack: List[String]): Boolean = {
      stack match {
        case Nil =>
          visited.addAll(visiting)
          visiting.foreach(result.push)
          visiting.clear()
          false
        case head :: tail if visited(head) => hasCycle(tail)
        case head :: tail =>
          graph(head).filterNot(visited) match {
            case Nil =>
              visited.add(head)
              visiting.remove(head)
              result.push(head)
              hasCycle(tail)
            case _ if visiting(head) => true
            case descendants =>
              visiting.add(head)
              hasCycle(descendants ++ tail)
          }
      }
    }

import scala.annotation.tailrec

private def sortTailRecMoreFunctional(
      graph: Map[String, List[String]]
  ): List[String] = {
    @tailrec
    def hasCycle(
        stack: List[String],
        visiting: Set[String],
        visited: Set[String],
        acc: List[String]
    ): (Boolean, Set[String], List[String]) = {
      stack match {
        case Nil => (false, visited ++ visiting, visiting.toList ++ acc)
        case head :: tail if visited(head) =>
          hasCycle(tail, visiting, visited, acc)
        case head :: tail =>
          graph(head).filterNot(visited) match {
            case Nil =>
              hasCycle(tail, visiting - head, visited + head, head :: acc)
            case _ if visiting(head) => (true, visited, acc)
            case descendants =>
              hasCycle(descendants ++ tail, visiting + head, visited, acc)
          }
      }
    }

    @tailrec
    def loop(
        xs: List[String],
        visited: Set[String],
        acc: List[String]
    ): List[String] = {
      xs match {
        case Nil => acc
        case head :: tail =>
          hasCycle(List(head), Set.empty, visited, acc) match {
            case (isCycle, visited, result) if !isCycle =>
              loop(tail, visited, result)
            case _ => Nil
          }
      }
    }

    loop(graph.keys.toList, Set.empty, List.empty)
  }

To summarize, I would like to underline a couple of points:

• topological sort is useful in any schedulers or calendars
• can be used for optimization in task scheduling
• is a useful tool in code representation in interpreters

For full code check GitHub