Graphs: directed graphs cycles

In software engineering there are lots of useful data structures. One of the useful structures is the graph. In this article I plan to take a directed graph and an algorithm for finding cycles.

What is a cycle?

A cycle is a path in which all vertices are unique except the first and last node.

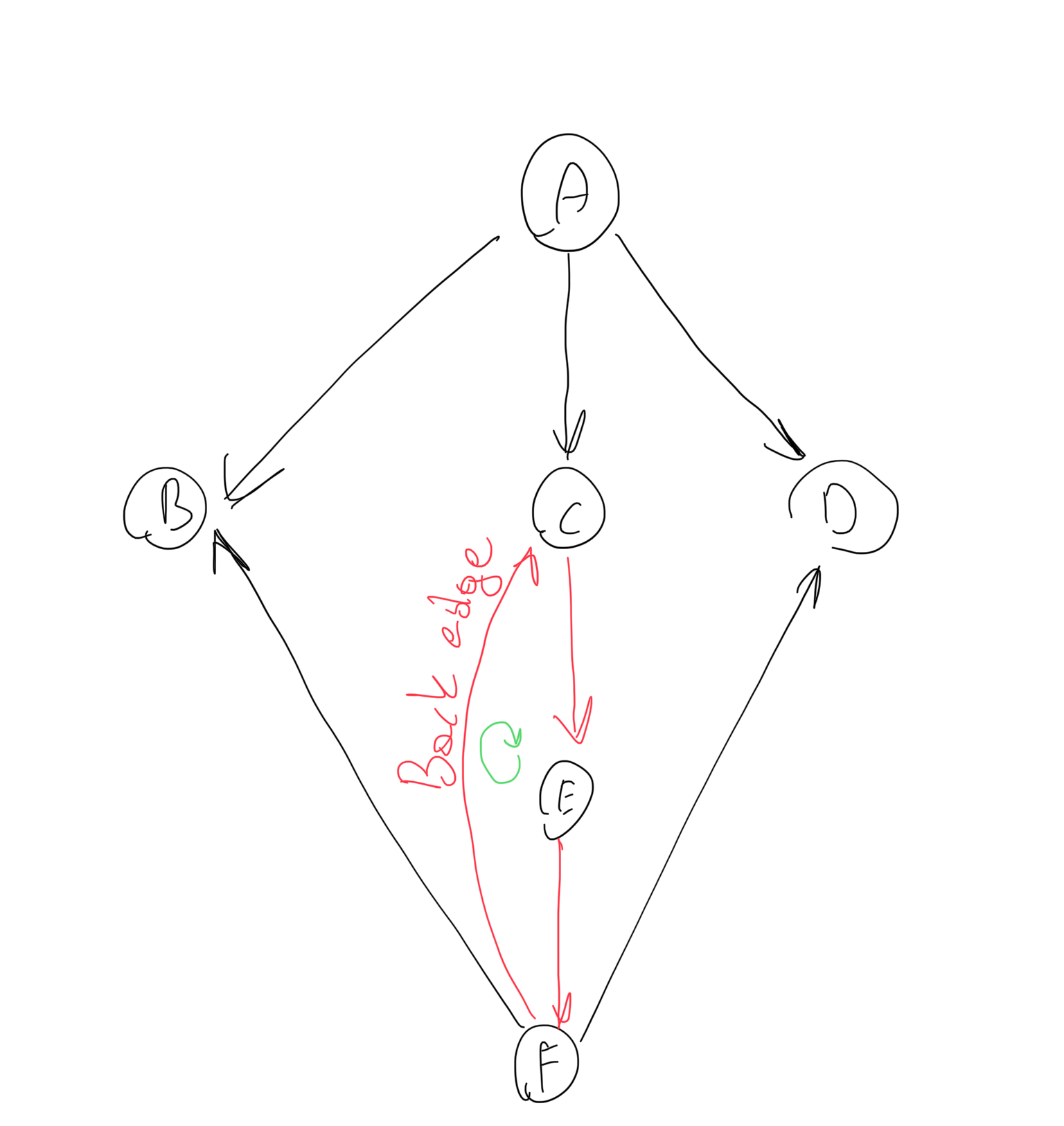
Example:

The cycle, path, is C -> E -> F -> C

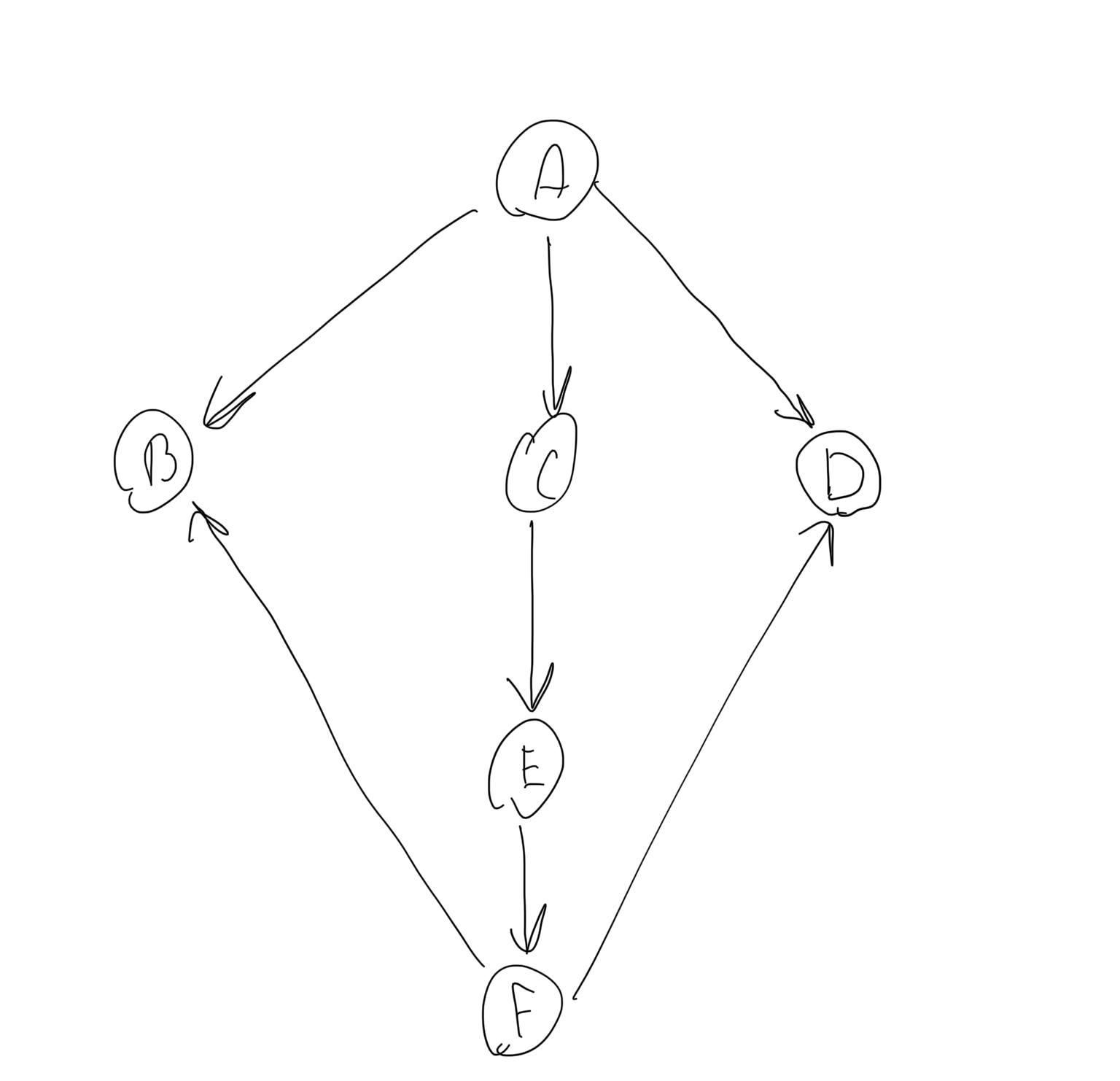
A directed graph that does not have a cycle is a directed acyclic graph, or DAG for short.

Example:

Going forward, let’s write some code that will check if a given graph has a cycle or is a DAG.

At the beginning, let’s discuss a little bit how to perform this task and make an algorithm sketch.

1. Start in any node
2. Mark node as gray, visiting
3. Visit node descendants
4. When node does not have any descendants mark as black, visited
5. When all descendants are black, visited, also mark node as visited
6. If any descendant during traversing the graph meets a gray (visiting) node, then a cycle exists
7. Repeat 1 - 6 starting for each node in graph

Simple visualization:

Then let’s implement it as simple recursion, DFS

import scala.collection.mutable
import scala.collection.mutable.{Stack, Set => MSet}

def hasCycleRec(graph: Map[String, List[String]]): Boolean = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]

    def checkCycle(node: String): Boolean = {
      if (visited.contains(node)) {
        false
      } else if (visiting.contains(node)) {
        true
      } else {
        visiting.add(node)
        for (n <- graph(node)) {
          if (checkCycle(n)) {
            return true
          }
        }

        visiting.remove(node)
        visited.add(node)
        false
      }
    }

    for (n <- graph.keys) {
      if (checkCycle(n)) return true
    }

    false
  }

However, recursion has stack size limitations, so let’s implement the algorithm in an iterative manner

import scala.collection.mutable
import scala.collection.mutable.{Stack, Set => MSet}

def hasCycleStackSafe(graph: Map[String, List[String]]): Boolean = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]
    val stack    = mutable.Stack.empty[String]

    for (n <- graph.keys) {
      stack.push(n)
      while (stack.nonEmpty) {
        val cn = stack.pop()
        if (!visited(cn)) {
          val descendants = graph(cn)
          if (descendants.isEmpty || descendants.forall(visited)) {
            visiting.remove(cn)
            visited.add(cn)
          } else if (visiting(cn)) {
            return true
          } else {
            visiting.add(cn)
            for (d <- descendants) {
              stack.push(d)
            }
          }
        }
      }
      visited.addAll(visiting)
      visiting.clear()
    }

    false
  }

But I am using Scala and I am not fully satisfied with this solution, so let’s make it using tail recursion:

import scala.annotation.tailrec
import scala.collection.mutable
import scala.collection.mutable.{Stack, Set => MSet}

def hasCycleTailRec(graph: Map[String, List[String]]): Boolean = {
    val visiting = MSet.empty[String]
    val visited  = MSet.empty[String]

    @tailrec
    def hasCycle(stack: List[String]): Boolean = {
      stack match {
        case Nil =>
          visited.addAll(visiting)
          visiting.clear()
          false
        case head :: tail if visited(head) => hasCycle(tail)
        case head :: tail =>
          graph(head).filterNot(visited) match {
            case Nil =>
              visited.add(head)
              visiting.remove(head)
              hasCycle(tail)
            case _ if visiting(head) => true
            case descendants         =>
              visiting.add(head)
              hasCycle(descendants ++ tail)
          }
      }
    }

    @tailrec
    def loop(xs: List[String]): Boolean = {
      xs match {
        case Nil                                   => false
        case head :: tail if !hasCycle(List(head)) => loop(tail)
        case _                                     => true
      }
    }

    loop(graph.keys.toList)
  }

Now is better, however it could be done more idiomatic and functional:

import scala.annotation.tailrec
import scala.collection.mutable
import scala.collection.mutable.{Stack, Set => MSet}


def hasCycleTailRecMoreFunctional(graph: Map[String, List[String]]): Boolean = {
    @tailrec
    def hasCycle(stack: List[String], visiting: Set[String], visited: Set[String]): (Boolean, Set[String]) = {
      stack match {
        case Nil => (false, visited ++ visiting)
        case head :: tail if visited(head) => hasCycle(tail, visiting, visited)
        case head :: tail =>
          graph(head).filterNot(visited) match {
            case Nil => hasCycle(tail, visiting - head, visited + head)
            case _ if visiting(head) => (true, visited)
            case descendants         => hasCycle(descendants ++ tail, visiting + head, visited)
          }
      }
    }


    def loop(xs: List[String], visited: Set[String]): Boolean = {
      xs match {
        case Nil => false
        case head :: tail => hasCycle(List(head), Set.empty, visited) match {
          case (isCycle, visited) if !isCycle => loop(tail, visited)
          case _ => true
        }
      }
    }


    loop(graph.keys.toList, Set.empty)
  }

I hope it will be useful not only in the recruitment process but also in the daily job ;)

For full code check GitHub